How do you find the value of the constant k in Coulomb's law?

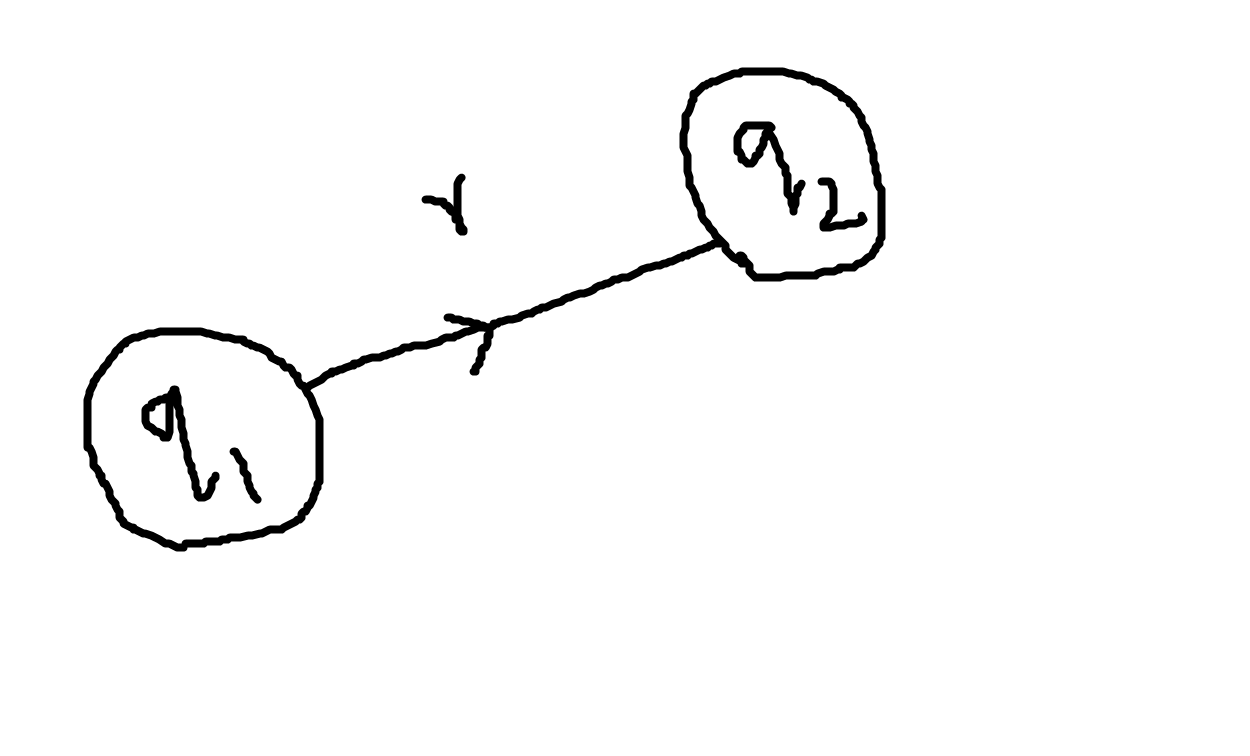
Coulomb force between two charges

Before we can understand what Coulomb's law is, we need to know about electric particles. If we know about electric charges, we can understand the force between them.

Coulomb's law is like Newton's force, but it is about electric particles that are invisible to our eyes. The force between two point electric particles that are stationary in a vacuum is called Coulomb's force.

According to Coulomb's law, if we want to know the force that can exist between two electric particles, it is the value obtained by the product of the magnitude of the two-point charges inversely proportional to the square of the distance between the two-point charges.

He would have said that the magnitude of the force between those two electric charges is this formula.

F = k q₁ q₂ /r²

This will not be confusing for everyone, but in Coulomb's law, he would have mentioned a constant value called K. He would have given some numbers for the value of this constant, i.e. he would have given a value of 9x10⁹ N m² C^-2.

He would have said that this constant value was created using this formula.

K = 1/4πԐ₀

 He would have conducted this entire study using a torsion balance. In his experiment, he would have conducted this study by considering the two charged spheres on which this torsion balance was placed as point electric particles and came to his conclusion.

 In this study, Coulomb's law applies only to point electric particles, so it is only a concept. Only if the size of the electric particles is small compared to the distance between them, the force between them can be found using Coulomb's law.

Coulomb conducted this study by considering the two charged spheres on which this torsion balance was placed as point electric particles in his experiment. The distance between the two spheres is much greater than the radii of the two spheres.

That is, the area formula of spheres is 1/4πr²

It means that the distance between two particles is squared and the inverse of the distance between them is given. So, taking these as the inverse of them, he would have created this constant by taking the product of the particles and the formula for the area of ​​their sphere by squaring its distance and the inverse of it, and the remaining formula would be the constant of the vacuum, Ԑ₀.